Cryptografie

6. Cryptografie#

Cryptografie is een overkoepelende term die je veel voor ziet komen in theoretische cybersecurity, en bestaat vooral uit wiskunde. Een thema in cryptografie is veilige data-overdracht.

Veilige data-overdracht gaat over het overdragen van berichten tussen twee punten (bijvoorbeeld twee personen), zonder dat iemand voor wie het bericht niet bedoeld was de inhoud ervan kan lezen. Het versleutelen van berichten op deze manier heet encryptie.

6.1. Praktische voorbeelden van encryptie#

Je hebt misschien vroeger wel eens samen met een vriend of vriendin een codetaal bedacht om berichten naar elkaar te sturen in de klas zonder dat de juf of meester wist wat er stond. Misschien was je codetaal om elk letter in het alfabet met 4 plekken te verschuiven, dus een ‘a’ wordt een ‘e’, een ‘b’ wordt een ‘f’ etc.

Als dit zo was, moet ik je helaas vertellen dat je niet de eerste persoon bent die hier mee kwam, want deze vorm van encryptie werd rond 50 BC (!) al gebruikt door Julius Caesar, en waarschijnlijk voor die tijd ook al. Dit encryptieschema heet het Caesarcijfer (Caesar cipher in het Engels), en vandaag de dag wordt het ook ROT genoemd.

Een ander voorbeeld is de one-time pad. De one-time pad werd tijdens de Tweede Wereldoorlog gebruikt door spionnen om berichten te versleutelen. De One-time pad bestaat uit je bericht, ook wel de “Plaintext” genoemd, en een “Geheime Sleutel” die alleen jij en de persoon naar wie je het bericht wilt sturen weten.

Er zijn twee versies van de one-time pad, eentje met cijfers waarbij het cijfer de positie van het getal in het alfabet aangeeft (Dus een A is een 1, B is een 2 etc.), en een versie waar bits gebruikt worden. In dat laatste geval zijn beide de plaintext en de sleutel in bits, dus eentjes of nulletjes. Dit betekent dus dat als je een bericht hebt met letters, je het eerst om moet zetten naar bits. Het versleutelen in de versie met bits ziet er als volgt uit:

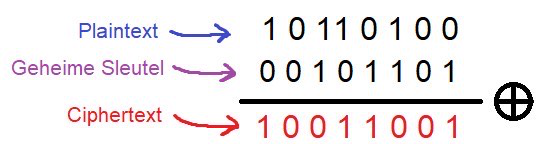
Voorbeeld van een versleuteling met 8 bits. De plaintext 10110100 wordt versleuteld met de geheime sleutel 00101101 en resulteert in de ciphertext 10011001.

Hier worden de plaintext en sleutel bit voor bit bij elkaar “opgeteld” met de XOR operatie. Dit staat voor “exclusive or” en betekent dat het resultaat 1 wordt als één van de twee opgetelde getallen 1 is, maar niet allebei:

  • \(1 \bigoplus 1 = 0\)

  • \(1 \bigoplus 0 = 1\)

  • \(0 \bigoplus 1 = 1\)

  • \(0 \bigoplus 0 = 0\)

Het resultaat heet de “ciphertext”. Deze ciphertext is een stuk onzin, en het betekent helemaal niks voor iemand die de sleutel niet heeft, maar iemand die hem wel heeft kan de plaintext weer uitrekenen door de ciphertext en de sleutel bij elkaar op te tellen. Probeer dit voor jezelf met de ciphertext en sleutel uit het voorbeeld hierboven. Als alles goed gegaan is, zou je de plaintext weer voor je moeten hebben. De bits worden vervolgens weer omgezet naar letters.

6.2. Slechte encryptie#

Het caesarcijfer wordt gezien als een slechte vorm van encryptie. Dit betekent dat een bericht dat versleuteld wordt met het caesarcijfer vaak makkelijk en snel gekraakt kan worden, dus zonder dat je weet hoeveel plekken je elke letter in het alfabet verschuift. Probeer voor jezelf of je deze ciphertext kan kraken: xopnozjovvs.

Inhoud